

Next: About this document ...
Definite and Indefinite Integral Practice
- Do the following integrals
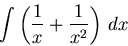 |
(1) |
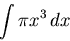 |
(2) |
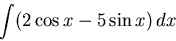 |
(3) |
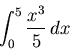 |
(4) |
- Do the following integral. Express your answer both
symbolically and numerically.
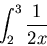 |
(5) |
- Without actually doing the two integrals, which of the following
is larger?
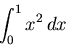 |
(6) |
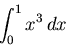 |
(7) |
- Evaluate the two integrals above and confirm your suspicions.
Dave Feldman
2001-01-12